Pearl of Chinese Mathematics Culture

——Ancient Chinese Algorithm System and Abacus

Li Wenlin, Researcher at the Academy of Mathematics and Systems Science (AMSS) of the Chinese Academy of Sciences (CAS)

It’s a great honor for me to participate in today's event to celebrate the 7th anniversary of successful inclusion of abacus skill into the list of world intangible heritages, and the forum.

I would like to deliver a speech entitled “Pearl of Chinese Mathematics Culture--Ancient Chinese Algorithm System and Abacus”. As President Liu Shangxi just said, Academician Wu Wenjun, a famous mathematician in China, first made it clear that from a historical view, there are two routes for the development of mathematics. The first route is based on Greece and reaches Europe through Arabia; the second route originates from China, and influences the development of global mathematics through India. This is the first time that Mr. Wu made it clear that there are two main routes for the development of mathematics.

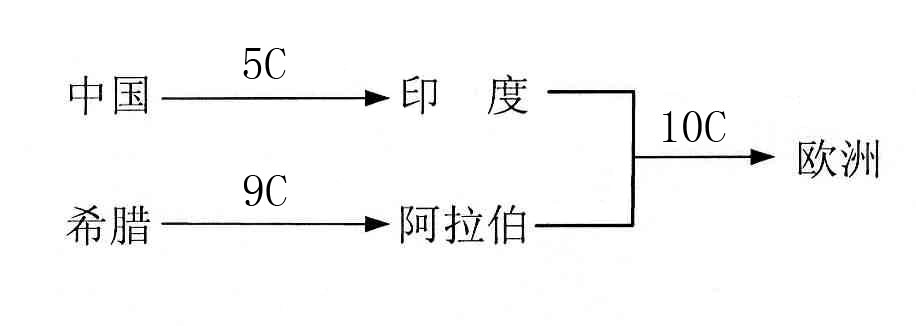
The following diagram is drawn by Academician Wu Wenjun to show two routes for the development history of mathematics in one of his papers, which is his first paper on the history of mathematics. On the Greek route, mathematics is mainly for proving theorems and logical reasoning. Now we call it a deductive tendency; while ancient Chinese mathematics route is based on the creation of algorithms, especially those for solving various equations, which is its main activity. I have summarized it as follows: One is the deductive tendency, mainly to prove theorems; the other is algorithmic tendency, mainly to create algorithms.

Ancient Chinese mathematics has obvious characteristics of algorithmization and mechanization. The algorithms mentioned here, in addition to simple operations of addition, subtraction, multiplication and division, include the creation of various algorithms. They are general computational programs summarized for the solution of a whole class of practical or scientific problems, and usually tend to be stylized, that is, to be applied mechanically.

So what is mechanization? In mathematics, mechanization has three characteristics: (i) Clarity, which means that the next step after completing one step is very certain and unambiguous; (ii) Finiteness, which means that certain results will be obtained within limited steps; (iii) Iterability, which means that it can be repeated iteratively.

Instead of being absolutely contradictory to Euclidean geometry deduction tendency, this algorithmic tendency of ancient and medieval Chinese mathematics complement with the latter and both are indispensable in the development history of mathematics. On the eve of the Renaissance, Eastern mathematics spread to Europe through the Arab region. Its fusion with Greek mathematics gave birth to modern mathematics.

The first point I want to talk about is that ancient Chinese mathematics and Greek mathematics originally belonged to two systems. The second part I want to talk about is the ancient Chinese algorithm system. The algorithm tradition of Chinese classical mathematics originated from Qin and Han dynasties, and reached its peak in Song and Yuan dynasties, forming a powerful and widely used algorithm system.

In my opinion, the concept of “algorithmic system” I proposed should mainly include three elements. (i) Various algorithms; (ii) Calculation tools; (iii) Calculation technology. The “calculation technology" here doesn’t refer to hardware computing technology, but mainly calculation methods, languages, etc., which correspond to what we call “software” today. The following part discusses three elements one by one.

First, “various algorithms”: Since Qin and Han dynasties, Chinese mathematicians have created a series of advanced algorithms (“Technique (Shu)” called by ancient Chinese mathematicians). The following are simple examples:

(1) Equations. The “Equations” in Volume 8 of the Nine Chapters on the Mathematical Art (about 2nd century BC) is an algorithm for solving linear simultaneous equations. The key algorithm of “Equations” is called “Multiplication and Successive Subtraction", which is highly mechanized. This method used to be called “Gaussian Elimination” in Western literatures. In recent years, Western scholars have begun to call it something else. For example, when I was a visiting professor at the University of Zurich, P.Gabriel, Academician of the French Academy of Sciences and former head of the Department of Mathematics at the University of Zurich suggested in his book he gave to me as a gift that the “Gaussian Elimination” referred to by Western mathematicians should be called “Zhang Cang Method” (Zhang Cang participated in the formulation of Nine Chapters on the Mathematical Art in the Han dynasty), which indicates the growing influence of Chinese algorithm tradition in the West; (2) In Song and Yuan dynasties, the “Positive and Negative Root Extraction” for solving higher order polynomial equations is Qin Jiushao Program (1247), which is also a highly mechanized algorithm, corresponding to the Western Horner algorithm (1819); (3) Zhu Sijie created the method for solving quaternary equations of higher order. In the west, it was not until the end of 18th century that E.Be- zout and other scholars in France began to systematically study this; (4) The "Chinese Remainder Theorem" for solving the system of first-order congruence equations was recovered independently by Euler and Gauss in the west in the 18th century; (5) Interpolation and “Zhao Cha Shu (Higher Order Interpolation)” created by Zhu Shijie in early Yuan Dynasty correspond to the Western Newton-Gregory formula.

Although we can’t list and explain all the algorithms of ancient Chinese mathematicians one by one in this paper, it’s not difficult to see from the above introduction that the algorithms created by ancient and medieval Chinese mathematicians are in line with the mechanization characteristics of “clarity”, “finiteness” and “iterability”. Many of these algorithms have reached a high level even by modern standards. Some of the mathematical truths expressed by these algorithms can only be recovered in Europe after the 18th century by relying on modern mathematical tools. These algorithms also have amazing complex structures. For example, the analysis of Qin Jiushao’s “Dayan Qiuyishu (One-order Congruence Group Solution)” and “Positive and Negative Root Extraction” indicate that, the calculation program of these algorithms contains the basic elements and structures of constructing nontrivial algorithms in modern computer languages. Academician Wu Wenjun has programmed the “Chinese Remainder Theorem”, and I have also programmed Liu Hui’s cyclotomic method. In the process of programming, we marveled at the mechanization degree of ancient Chinese algorithms. To sum up, the prosperity of ancient Chinese algorithms constitutes the mainstream of mathematical development. Then, these rich and complex algorithms certainly will call for improvements in calculation tools.

(2) “Calculation tools”: Since the Spring and Autumn Period and the Warring States Period, the Chinese have been using counting rods for a long time, and constantly looking for new calculation tools at the same time. In Zhen Luan's “Book of Mathematics” alone, there recorded as many as 14 kinds of arithmetic tools. The modern form of abacus, i.e., the abacus with beams and gears, that appeared and standardized until the Ming dynasty has become a stable and effective calculation tool in the Chinese classical algorithm system.

(3) “Calculation technology”: China has been using operation rhyme formulas for a long time, which perhaps is attributable to the language characteristics. The multiplication formula appeared as early as the Warring States period, which was used as a language for multiplication and division in the calculation system (equivalent to arithmetic software). Various formulas had prevailed since the Mid-Tang dynasty, gradually forming a mechanized language suitable for four arithmetic operations and higher order operations of the abacus system.

These are three elements that contribute to the formation of the Chinese classical algorithm.

Finally, I would like to discuss with you why abacus is a unique product of the Chinese classical algorithm system. I personally think that there are three necessary conditions for the formation of an abacus: First, the need for calculation tools; second, the decimal value system, especially the system of counting decimal numbers; third, mechanization of the computational process. Specific discussions are as follows.

First, the need for calculation tools is reflected in both mathematics and practice. (i) Advanced algorithms have been developed, which objectively proposed a need for improving calculation tools; (ii) From the mid-Tang dynasty to Song and Yuan dynasties, the commercial economy was flourishing after unprecedented development, which was also reflected in Riverside Scene at Qingming Festival and other works.

Second, the decimal numeration system represents an indelible contribution to human civilization. Without the decimal value system, we can’t imagine what our mathematics would look like today. The French mathematician Pierre-Simon Laplace once highly praised the invention of the decimal value system, and said that it “makes our arithmetic system top-notch among all useful creations.” Ancient Chinese mathematicians constructed the “Oriental Mathematics Building” with algorithmic characteristics on the basis of strictly following the calculation system of the decimal value system. Among ancient civilizations of the world, only China and India used the decimal value system. Ancient Egypt and Greece adopted the decimal counting system other than the bit value counting system; ancient Babylon adopted the bit value counting system instead of the decimal counting system. In ancient China, the decimal value system appeared at a very early date. For example, in the Spring and Autumn Period and Warring States Period, the counting symbol of the rod-arithmetic decimal value system appeared on the knife coin. The Sun Zi's Mathematical Manual provided specific and explicit counting rules for the decimal value system. India is also the earliest country in the world to use the decimal value system for counting, which appeared later than that in China. According to the Bakhshali Manuscript, the integer decimal value system appeared in India in the 3rd to 4th century AD. Moreover, the decimal value system of ancient India used dot notation to indicate "zero", which is more advanced than ancient China that used null.

However, for abacus, only the integer representation in the decimal system is not enough, and the fractional representation is also required. In China, as early as the Liu Hui’s era, there appeared complete fractional representation of the decimal value system. Liu Hui made notes on “Root Extraction” in Chapter Shao Guang of Nine Chapters on the Mathematical Art: “...When the square root can’t be extracted, it is expressed in decimal fractions. Below the ones digit, one-digit abdication is one tenth, and two-digit abdication is one hundredth, and so on in a similar way. The numbers lost are insignificant.” It means that, when representing an irrational number, if the integer is not enough, one decimal place will be added. If it’s still not enough, continue to move backward by one more place...; until the end, although part of it is lost, what is lost is insignificant. Liu Hui's ideas were ahead of their times. The representation of decimal decimals had undergone a long-term development process, but by the Tang dynasty, decimal decimals had been gradually applied, creating conditions for final invention of the abacus. In Europe, it was not until the 16th century that the Dutch mathematician Steven first advocated the use of decimal fractions in his book Decimal Arithmetic, making a milestone in the history of European mathematics. Since European numeration was introduced from India and Arabia, we can't help but wonder why the system didn't spread to Europe at the beginning of the Renaissance, but was reinvented by Steven in the 16th century, if the decimal had been invented in India. One possible reason is that India didn’t produce decimal fractions. For this reason, I looked up relevant information, and found that there is no record of the use of decimal fractions in Indian mathematical and astronomical works. We can see this conclusion in the General History of Mathematics written by V. Katz, American mathematics historian. Therefore, in contrast, we can conclude that China's use of decimal fractions is very advanced.

Third, mechanization of the computational process. We have introduced the mechanized nature of various algorithms above. In order to explain relevant problems more clearly, we took the cyclotomic method as an example to illustrate the mechanized nature of Chinese classical algorithms. Liu Hui’s cyclotomic method started from a hexagon, to a dodecagon and a twenty-four-sided shape... As the number of sides within a circle is increasing, its area and circumference are getting closer to a circle. Liu Hui got Pi 3.14 on 192 sides and Pi 3.1416 on 3,072 sides. Liu Hui's algorithm is very simple, that’s, using the Pythagorean Theorem to continuously approach a more accurate pi; this algorithm has distinctive features (see the Figure below). In their textbooks, many middle schools use Liu Hui's cyclotomic method as an example to help students understand the concept of “algorithm”.

In addition to the mechanization of algorithms, there is also the mechanization of basic calculations, manifested as rhyme formulas in the abacus system.  In particular, the generation of division rhyme formulas has mechanized the division operation from estimating quotients to formula quotients. In Yuan and Ming dynasties, rhyme formulas had been applied for addition, subtraction, multiplication and division in an all-round manner, that is, all-round mechanization.

The above are several elements and conditions for the emergence of Chinese abacus.

In contemporary times, we have entered a new period from abacus to abacus and mental arithmetic. In the period of abacus, estimation and mental arithmetic didn’t have mechanized characteristics. In order to learn about the mental arithmetic component of ancient Indian calculations, I looked up the calculation methods of ancient India. A Japanese expert mentioned in his book that, the Indians had abacus beads in early days, but didn’t develop later; a painting found in a grotto in India showed the image of Indian calculations--they used a wooden board (sometimes covered with leather), and wrote on it with something similar to chalk. The writing can be erased, and contained many mental arithmetic elements. Indians may be faster at adding and subtracting by hand and in their heads, but slower than abacus in terms of multiplication and division.

Upon comparison, we learned that abacus is a unique product of the Chinese classical algorithm system. Chinese civilization is the only one that has lasted for thousands of years without interruption, while the abacus skill and abacus are one of the cultural heritages that have been inherited and energetic until today along with this long civilization. We shall cherish and protect this heritage, and make good use of it in the socialist modernization cause with Chinese characteristics.

These are some of my views. Your criticism and correction are welcome. Thank you.

Experts who make comments: Guo Shuchun, Professor of Institute for the History of Natural Sciences (IHNS), Chinese Academy of Sciences

Professor Li’s report accurately elaborated on the background of abacus, as well as the algorithm system and language evolved from ancient Chinese mathematics. Professor Li began by quoting Mathematician Wu Wenjun, which was put forward for refuting the denial of the international status of Chinese mathematics by some western mathematics historians. Against this backdrop, Mr. Wu Wenjun proposed that two mathematics development routes of China and Greece have alternately become the mainstream in this regard globally. This understanding is particularly important.

At the conference to celebrate the 1st anniversary of successful inclusion of abacus skill into the list of world intangible heritages, I pointed out in my speech that, it’s a great delight for everyone that the abacus has been included into the list of world intangible heritages. But there are still difficulties in publicizing it not only to foreigners but also to the Chinese. A few years ago, we compiled a book entitled Important Scientific Inventions and Creations in Ancient China. When soliciting the opinions from foreign scholars, a foreign expert held that abacus should be removed, because Roman once used abacus; although Roman abacus clearly can’t be compared with Chinese abacus, such misunderstandings indicate that in terms of abacus promotion, we still have a long way to go.

Mathematician Wu Wenjun’s views are of great importance for us. It’s very difficult but important for abacus to be understood by the Chinese and even by people all over the world. To succeed in this, there is still a long way to go, which requires joint efforts of abacus practitioners. Professor Li has given us an exciting and inspiring speech. Due to time limit, I will stop now.